Что такое связанные ранги - Коэффициент ранговой корреляции Кендалла - Математическая

До сих пор мы анализировали зависимости между количественными переменными, измеренными в так называемых количественных шкалах, то есть в шкалах с непрерывным множеством значений, позволяющих выявить, на сколько или во сколько раз проявление признака у одного объекта больше меньше , чем у другого например, производительность труда, себестоимость продукции и т. Вместе с тем на практике часто встречаются с необходимостью изучения связи между ординальными порядковыми переменными, измеренными в так называемой порядковой шкале. В этой шкале можно установить лишь п о ряд о к, в котором объекты выстраиваются по степени проявления признака например, качество жилищных условий, тестовые баллы, экзаменационные оценки и т.

Ранговая корреляция

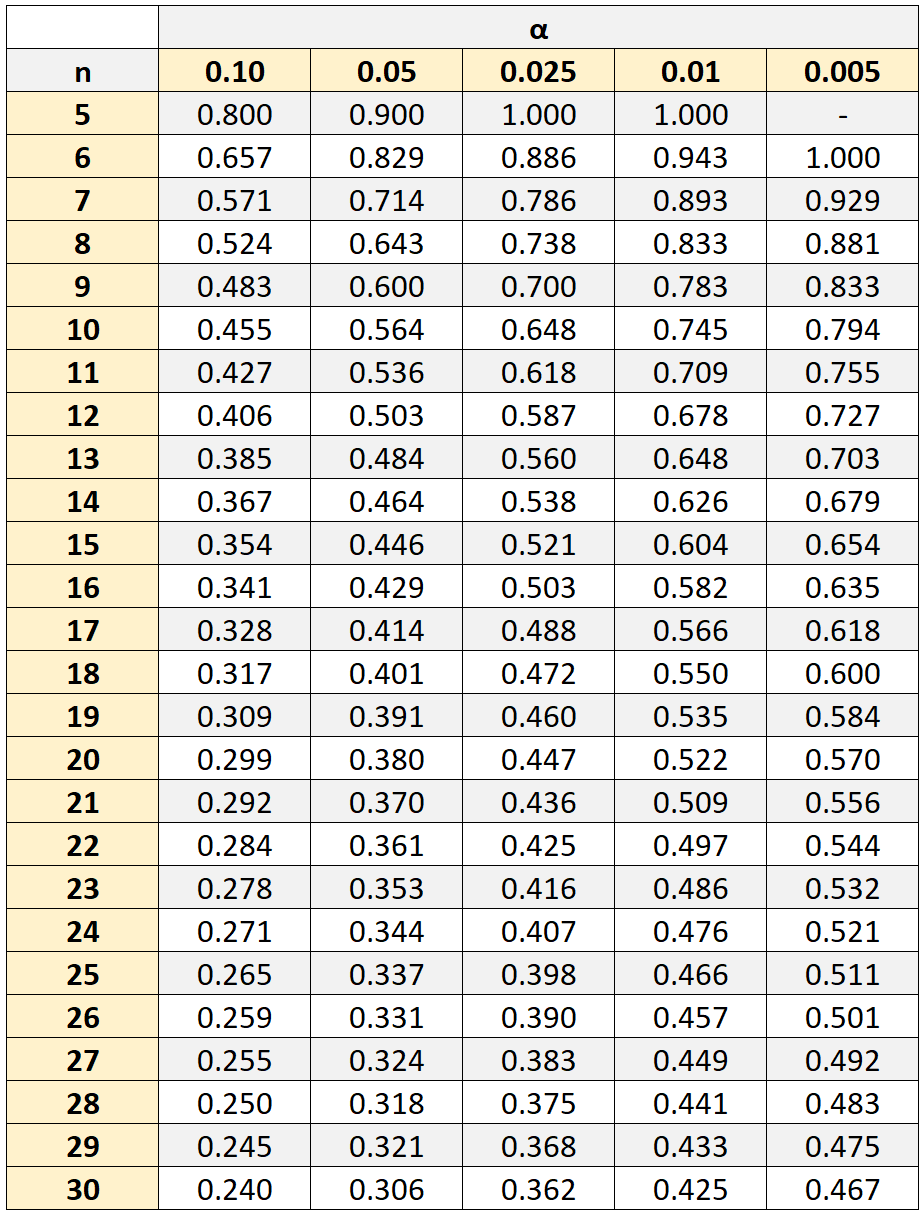
Можно оценивать связь между двумя качественными признаками, используя коэффициент ранговой корреляции Кендалла. Введем обозначение суммы рангов R. Замечани е. При достаточно большом объеме выборки и при значениях коэффициентов ранговой корреляции, не близких к единице, имеет место приближенное равенство.

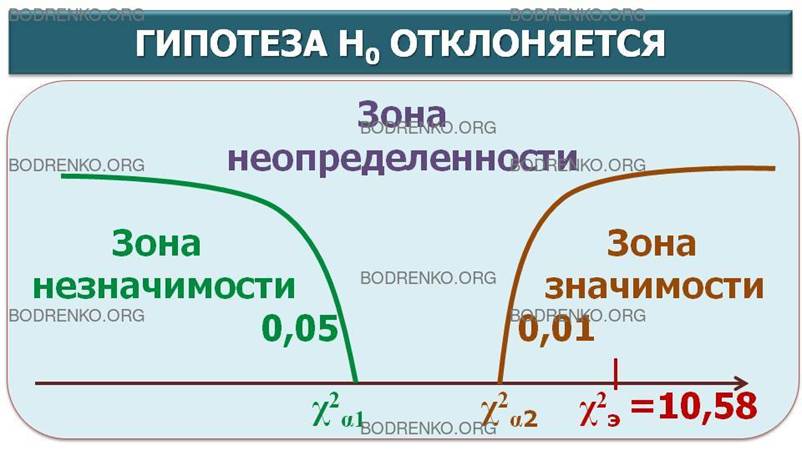
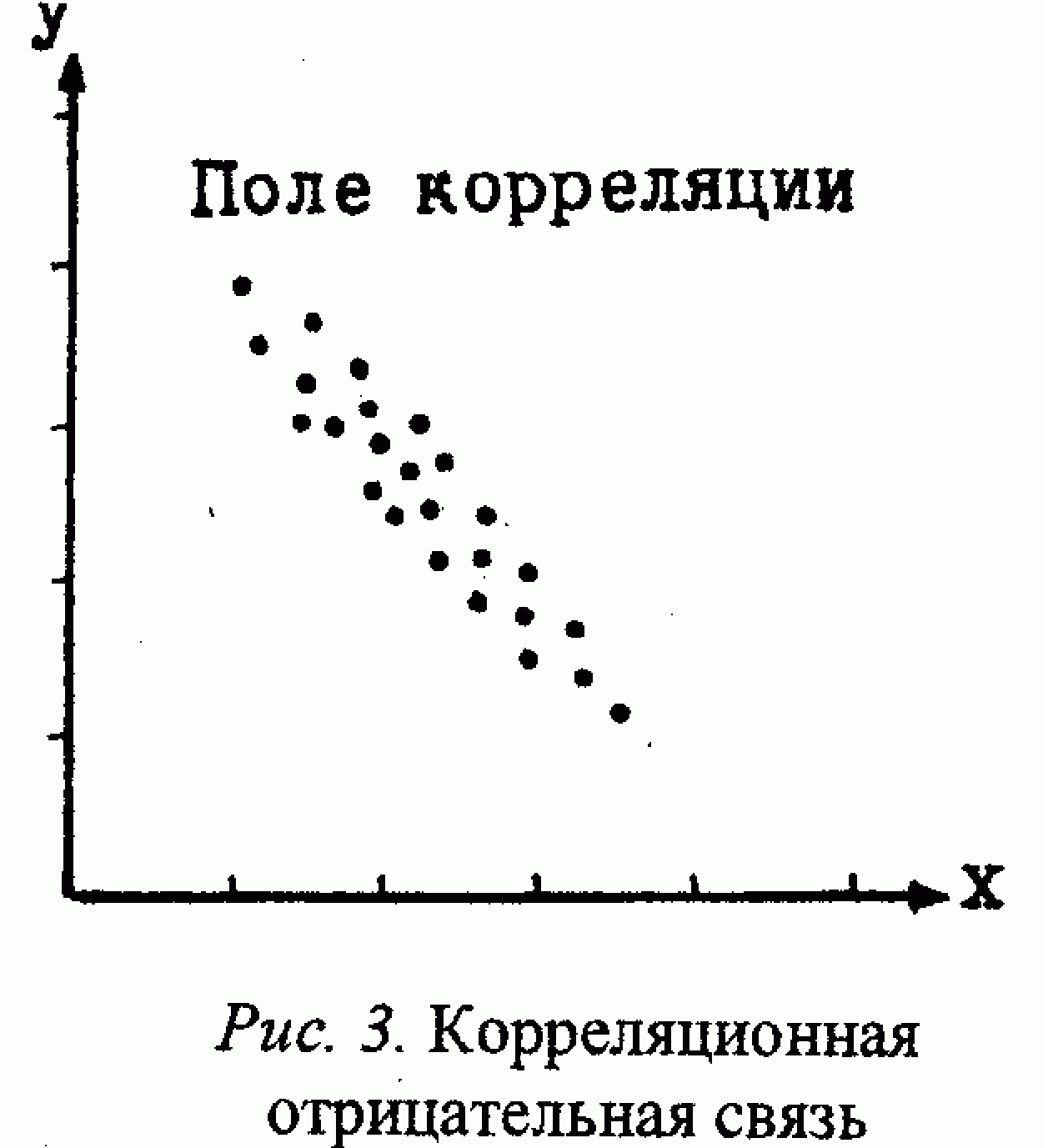
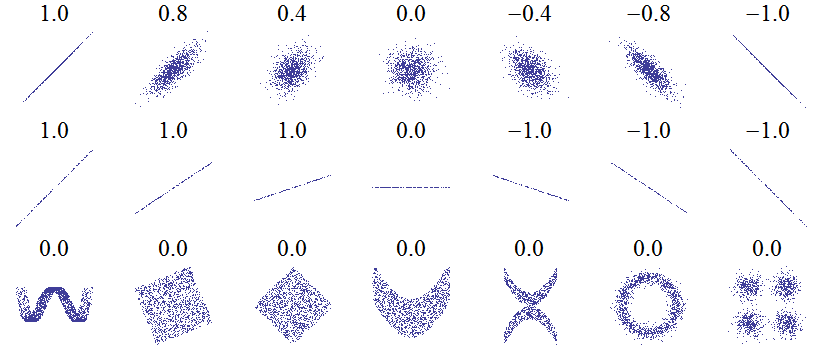
Коэффициент корреляции - это статистический показатель зависимости двух случайных величин. Коэффициент корреляции - это корреляцинное отношение, математическая мера корреляции двух случайных величин. В случае, если изменение одной случайной величины не ведёт к закономерному изменению другой случайной величины, но приводит к изменению другой статистической характеристики данной случайной величины, то подобная связь не считается корреляционной , хотя и является статистической. Коэффициент корреляции - это мера линейной зависимости двух случайных величин в теории вероятностей и статистике. Некоторые виды коэффициентов корреляции могут быть положительными или отрицательными. В первом случае предполагается, что мы можем определить только наличие или отсутствие связи, а во втором - также и её направление.

• Как и в случае КРК Спирмена исходные данные представляют собой две выборки, каждая из которых содержит n последовательных и несвязанных рангов, то есть чисел от 1 до n. Кендалл построил свой коэффициент корреляции на количестве пар рангов, которые упорядочиваются в одинаковом направлении как по переменной х, так и по переменной у.
• В случае, когда силу зависимости между случайными величинами невозможно определить численно при помощи обычного коэффициента корреляции , используют ранговую корреляцию , которая имеет дело не с непосредственными значениями, а с рангами порядковыми номерами. Наиболее часто используют коэффициент ранговой корреляции Спирмена , вычисление которого можно разбить на этапы:.
• В случае если изменение одной случайной величины не ведёт к закономерному изменению другой случайной величины, но приводит к изменению другой статистической характеристики данной случайной величины, то подобная связь не считается корреляционной, хотя и является статистической [3].

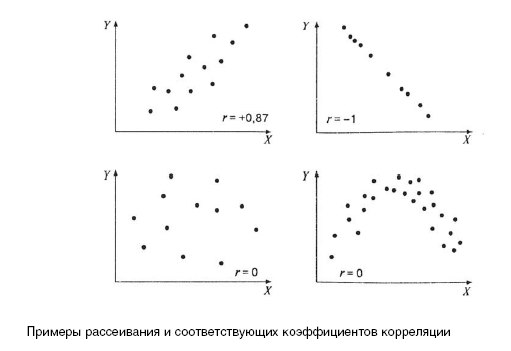
Корреляционный анализ - статистический инструмент анализа многомерных данных. Основная проблема, решаемая этим инструментом, - нахождение скрытых значимых зависимостей между переменными атрибутами. Силу корреляции можно измерить абсолютным значением коэффициента корреляции. Знак коэффициента корреляции также обозначает прямую или обратную зависимости между переменными. Если расчет проводился с числовыми данными с упорядоченными мерами, то следует использовать меры ранговой корреляции Спирмана или Кенделла.

Похожие статьи

• Беременная коза перестала есть что делать
• Украсить чехол для телефона своими руками - Схемы как связать чехол для телефона своими руками
• Болит пломбированный зуб что делать
• Что такое модельные прически - Более 25 лучших идей на тему «Короткие женские стрижки» на